Published on
Mon 07 October 2019
by
myst404 (@myst404_)
Edited on
Wed 09 October 2019
TL;DR: Magic hashes are well known specific hashes used to exploit Type Juggling attacks in PHP. Combined with bcrypt limitations, we propose the concept of Super Magic Hashes. These hashes can detect 3 different vulnerabilities: type juggling, weak password storage and incorrect Bcrypt usage. A Go PoC found some MD5, SHA1 and SHA224 super magic hashes.
Introduction
Type Juggling issues in PHP and Magic Hashes are known since at least 2014. As a quick reminder, in PHP two strings matching the regular expression 0+e[0-9]+ compared with == returns true:
'0e1' == '00e2'== '0e1337' == '0'
Indeed all these strings are equal to 0 in scientific notation.
These hashes can be used to detect weak authentication systems. Using the @spazef0rze example, we could detect a type juggling issue combined to a weak (MD5) password storage:
php > var_dump(md5('240610708') == md5('QNKCDZO'));
bool(true)
Bcrypt has known limitations. One of them is that passwords are truncated on NUL bytes.
Of course, nobody (?) uses NUL bytes in his password.
However, such character can easily appear when the raw output of a hash is used. Why pre-hash before using bcrypt? To prevent the other limitation: passwords are truncated at 72 characters in bcrypt. Using the Paragon Initiative example, we could detect the NUL byte limitation.
Both 1]W and @1$ produce a SHA-256 hash output that begins with ab00. The password comparison will be considered as true:
php > $pass1 = '1]W';
php > $pass2 = '@1$';
php > $stored_hash = password_hash(hash('sha256',$pass1, true), PASSWORD_DEFAULT);
php > var_dump(password_verify(hash('sha256', $pass2, true), $stored_hash));
bool(true)
Note that here we passed true as an argument to the hash function to output raw binary data.
Time to merge! We can test both cases if we can find hashes matching 00+e[0-9]+. For example, with MD5:
php > $pass1 = 'KnCM6ogsNA1W';
php > $pass2 = '&rh1ls6cl&G4';
php > echo hash('md5', $pass1);
00e73414578113850089230341919829
php > echo hash('md5', $pass2);
00e48890746054592674909531744787
php > var_dump(hash('md5', $pass1) == hash('md5', $pass2)); #Magic Hash
bool(true)
php > var_dump(password_verify(hash('md5',$pass1, true), password_hash(hash('md5',$pass2, true), PASSWORD_DEFAULT))); #Bcrypt limitation
bool(true)
Tests were performed with PHP 7.2.19.
Because these magic hashes are enhanced versions from the normal ones, they are some sort of super magic hashes.
Let's try to find these super magic hashes!
A bit of math
If you do not care about maths, you can just skip this section.
Finding super magic hashes is not trivial for hashing functions with a long output. The hashes need to start by at least two 0 followed by the letter e and then only numbers.
MD5 and SHA1 are easy to find so let's focus on the SHA224 algorithm.
The SHA224 digest output is 56 characters in hexadecimal representation (224 bits). So, the probability to find a super magic hash for a given random password is:
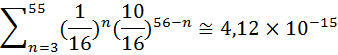
Reminder: we are looking for hashes like
00e12345678901234567890123456789012345678901234567890123
000e1234567890123456789012345678901234567890123456789012
0000e123456789012345678901234567890123456789012345678901
...
000000000000000000000000000000000000000000000000000000e1
What are our chances of finding an interesting hash after many calculations?
We are looking for the probability to get at least one magic hash depending on the number of hashes calculated. We can use the following code to draw the graph of probabilities:
#!/usr/bin/python2
# -*- coding: utf-8 -*-
from __future__ import division
import scipy.stats as stats
import matplotlib.pyplot as plt
import numpy as np
nb_hashs = 1E16
proba_by_hash = 0
for n in range(3,55):
proba_by_hash = proba_by_hash +(1/16)**n*(10/16)**(56-n)
def proba(i):
return 1-stats.binom.cdf(0,i,proba_by_hash)
x = np.linspace(0,nb_hashs,100000)
plt.plot(x,map(proba,x))
plt.xscale('log')
plt.xlabel('Number of hashes calculated')
plt.ylabel('Probability')
plt.show()

It does not work :(
Because of the small probability of success, the binomial calculation fails. We need to use a binomial approximation, for example the tyrtamos one.
The probability to get a SHA224 super magic hash for a random password is: 4.12e-15. Here is the probability to get at least one super magic hash depending on the number of hashes calculated (logarithmic scale):
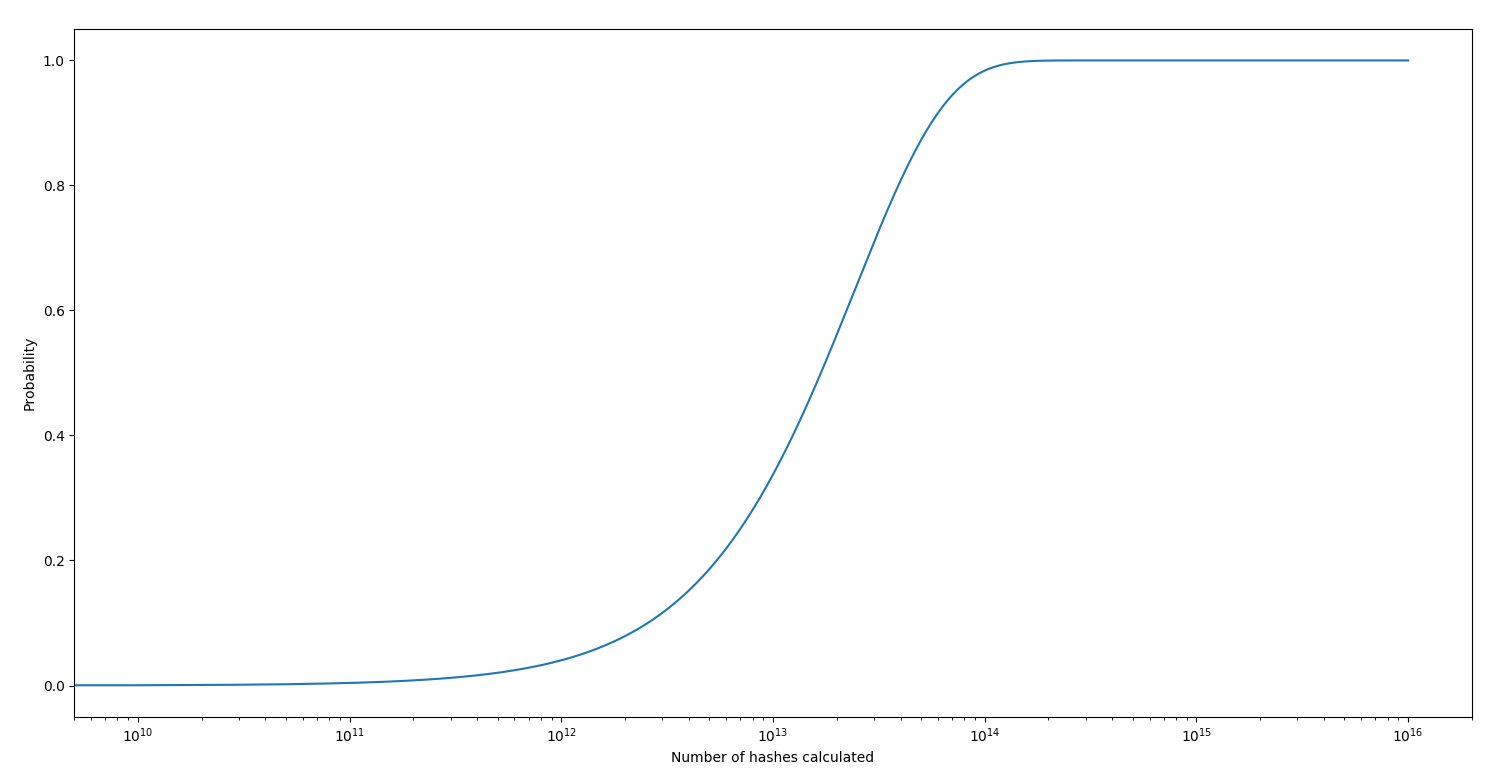
You need to calculate roughly 1,61e14 hashes to have 50% to get at least 1 super magic hash.
The probability to get a SHA224 magic hash for a random password is: 4.12e-14. Here is the probability to get at least one magic hash depending on the number of hashes calculated (logarithmic scale):
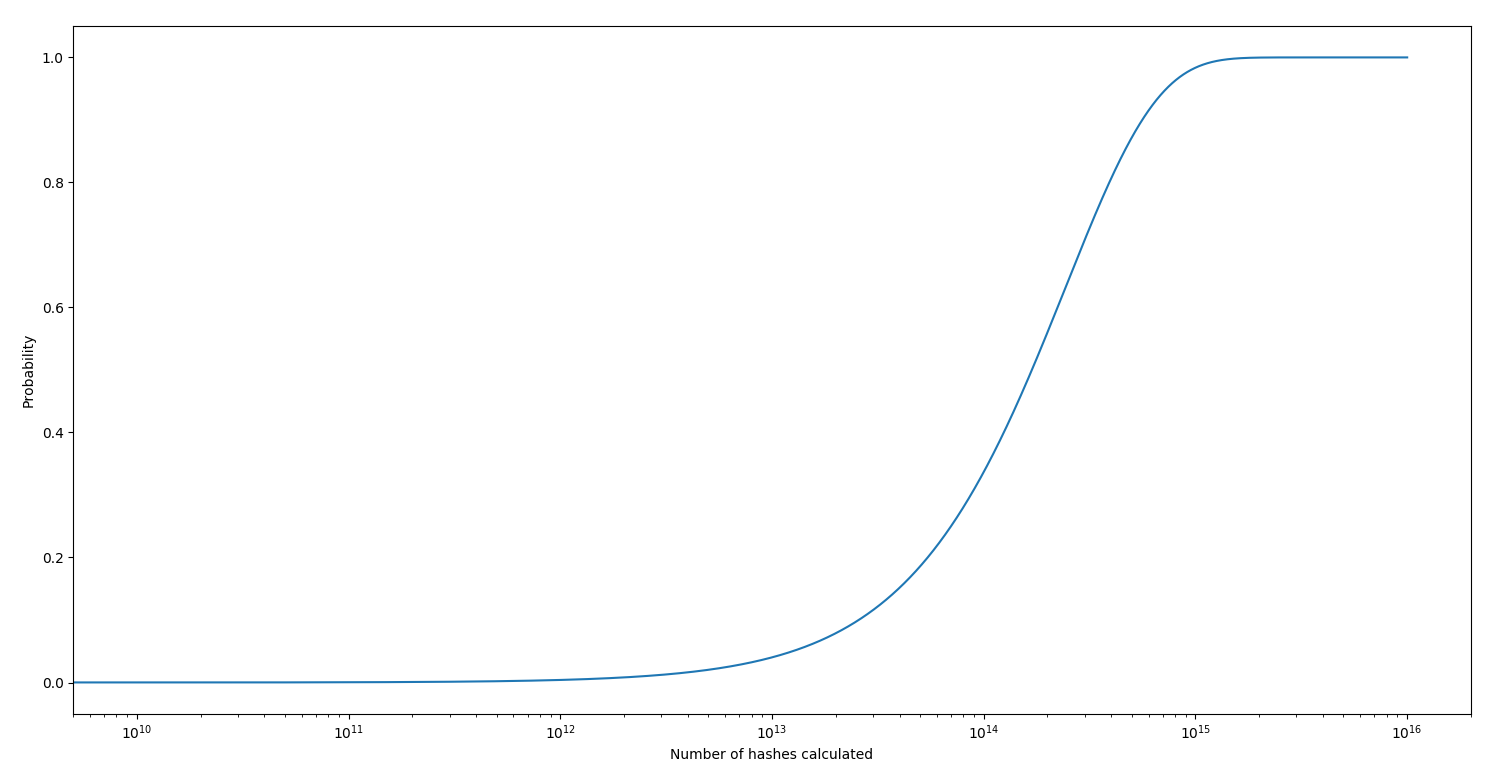
You need to calculate roughly 1,61e13 hashes to have 50% to get at least 1 magic hash.
Note that super magic hashes are 10 times less likely than magic hashes.
Python script to plot the graphs.
Golang PoC
This part is about optimizing a Go script.
For a quick PoC I decided to use the Go language. To be as efficient as possible we will use the nice benchmark functionality of Golang. We will also use the testing function to be sure that the hash parsing function we create does not miss (super) magic hashes.
Our requirements for the PoC are:
- Be as fast as possible
- Look for magic (0e) and super (00+e) magic hashes
- Find passwords that can pass password policies
- Valid for the SHA224 hash but can be adapted easily to other hashing algorithms
- CPU only so it can run on some unused VPS
The benchmarks were made on my Ubuntu 18.04.3 laptop, i7-8550U CPU @ 1.80GHz, Go version 1.10.4.
The trivial PoC looks like this. We just generate a random password and compare it to a Regular Expression:
var re = regexp.MustCompile(`^0+e\d*$`)
const letterBytes = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789&~#'{([-|_@)]=}+$*!:;,?./"
var test1 = "0e123456789012345678901234567890123456789012345678901234";
var test2 = "00e12345678901234567890123456789012345678901234567890123";
var test3 = "1e123456789012345678901234567890123456789012345678901234";
var test4 = "0e12345678901234567890123456789012345678901234567890123a";
func TestParsing(t *testing.T) { //test that our parsing function is valid
if !Parse_1(test1) || !Parse_1(test2) || Parse_1(test3) || Parse_1(test4) {
t.Error("Parsing Error")
}
}
func rand_1(strSize int) string { //generate a random password that could pass password policies
var bytes = make([]byte, strSize)
rand.Read(bytes)
for k, v := range bytes {
bytes[k] = letterBytes[v%byte(len(letterBytes))]
}
return string(bytes)
}
func hash_sha224(password string) string { //generate the SHA224, return the hex representation
h := sha256.New224()
h.Write([]byte(password))
bs := h.Sum(nil)
hash := fmt.Sprintf("%x\n", bs)
return string(hash)
}
func Parse_1(h string) bool { //test whether the generated hash is a (super) magic one
if (re.FindString(h) != "") {
return true
}
return false
}
func BenchmarkParse_1(b *testing.B) {
for n := 0; n < b.N; n++ {
r := rand_1(8)
hash := hash_sha224(r)
if Parse_1(hash) {
fmt.Println(r)
fmt.Println(hash)
fmt.Println("")
}
}
}
Let's run the benchmark:
$ go test -bench . -benchmem -benchtime=5s -v
=== RUN TestParsing
--- PASS: TestParsing (0.00s)
goos: linux
goarch: amd64
BenchmarkParse_1-8 10000000 742 ns/op 280 B/op 7 allocs/op
It means that for 10M hashes generated and checked, the mean time is 742 nanoseconds per operations, the number of bytes allocated is 280 per operation and there are 7 allocations per operation.
Thanks to this Stackoverflow post, we can find a faster random password generator:
var src = rand.NewSource(time.Now().UnixNano())
const (
letterIdxBits = 6 // 6 bits to represent a letter index
letterIdxMask = 1<<letterIdxBits - 1 // All 1-bits, as many as letterIdxBits
letterIdxMax = 63 / letterIdxBits // # of letter indices fitting in 63 bits
)
func rand_2(strSize int) string {
bytes := make([]byte, strSize)
// A src.Int63() generates 63 random bits, enough for letterIdxMax characters!
for i, cache, remain := strSize-1, src.Int63(), letterIdxMax; i >= 0; {
if remain == 0 {
cache, remain = src.Int63(), letterIdxMax
}
if idx := int(cache & letterIdxMask); idx < len(letterBytes) {
bytes[i] = letterBytes[idx]
i--
}
cache >>= letterIdxBits
remain--
}
return *(*string)(unsafe.Pointer(&bytes))
}
func BenchmarkParse_2(b *testing.B) {
for n := 0; n < b.N; n++ {
r := rand_2(8)
hash := hash_sha224(r)
if Parse_1(hash) {
fmt.Println(r)
fmt.Println(hash)
fmt.Println("")
}
}
}
New benchmark:
$ go test -bench . -benchmem -benchtime=5s -v
=== RUN TestParsing
--- PASS: TestParsing (0.00s)
goos: linux
goarch: amd64
BenchmarkParse_1-8 10000000 742 ns/op 280 B/op 7 allocs/op
BenchmarkParse_2-8 10000000 663 ns/op 272 B/op 6 allocs/op
Roughly 11% faster and one less allocation, it's a quick win. We can do better. Instead of creating a new type hash each time, we can reuse it:
func BenchmarkParse_3(b *testing.B) {
h := sha256.New224()
for n := 0; n < b.N; n++ {
r := rand_2(8)
h.Reset()
h.Write([]byte(r))
bs := h.Sum(nil)
hash := fmt.Sprintf("%x\n", bs)
if (re.FindString(string(hash)) != "") {
fmt.Println(string(r))
fmt.Println(string(hash))
fmt.Println("")
}
}
}
Benchmark:
$ go test -bench . -benchmem -benchtime=5s -v
=== RUN TestParsing
--- PASS: TestParsing (0.00s)
goos: linux
goarch: amd64
goarch: amd64
BenchmarkParse_1-8 10000000 742 ns/op 280 B/op 7 allocs/op
BenchmarkParse_2-8 10000000 663 ns/op 272 B/op 6 allocs/op
BenchmarkParse_3-8 10000000 657 ns/op 144 B/op 5 allocs/op
1% faster, one less allocation, and nearly 2 times less memory manipulated: nice! However, in this scenario we generate a random password formatted as a string converted to bytes in order to calculate the hash. It corresponds to the following lines in our code:
r := rand_2(8)
h.Reset()
h.Write([]byte(r))
We change to random password function to return bytes:
func rand_3(n int) []byte {
b := make([]byte, n)
// A src.Int63() generates 63 random bits, enough for letterIdxMax characters!
for i, cache, remain := n-1, src.Int63(), letterIdxMax; i >= 0; {
if remain == 0 {
cache, remain = src.Int63(), letterIdxMax
}
if idx := int(cache & letterIdxMask); idx < len(letterBytes) {
b[i] = letterBytes[idx]
i--
}
cache >>= letterIdxBits
remain--
}
return *(*[]byte)(unsafe.Pointer(&b))
}
func BenchmarkParse_4(b *testing.B) {
h := sha256.New224()
for n := 0; n < b.N; n++ {
r := rand_3(8)
h.Reset()
h.Write(r)
bs := h.Sum(nil)
hash := fmt.Sprintf("%x\n", bs)
if (re.FindString(string(hash)) != "") {
fmt.Println(string(r))
fmt.Println(string(hash))
fmt.Println("")
}
}
}
Benchmark:
$ go test -bench . -benchmem -benchtime=5s -v
=== RUN TestParsing
--- PASS: TestParsing (0.00s)
goos: linux
goarch: amd64
BenchmarkParse_1-8 10000000 742 ns/op 280 B/op 7 allocs/op
BenchmarkParse_2-8 10000000 663 ns/op 272 B/op 6 allocs/op
BenchmarkParse_3-8 10000000 657 ns/op 144 B/op 5 allocs/op
BenchmarkParse_4-8 10000000 637 ns/op 136 B/op 4 allocs/op
Roughly 3% faster and one less allocation, we need to improve the slowest operation: the parsing function. Instead of working on regular expressions, we are going to check directly the bytes of the hash calculation output:
func Parse_2(h []byte) bool {
if h[0] == 0 || h[0] == 14 { //check whether the hash starts by 00 or 0e
for _, x := range h[1:] {
switch x { //all unexpected bytes return false (https://ascii.cl/conversion.htm)
case
10, 11, 12, 13, 15, //0A to 0F
26, 27, 28, 29, 31, //1A to 1F
42, 43, 44, 45, 47, //2A to 2F
58, 59, 60, 61, 63, //3A to 3F
74, 75, 76, 77, 79, //4A to 4F
90, 91, 92, 93, 95, //5A to 5F
106, 107, 108, 109, 111, //6A to 6F
122, 123, 124, 125, 127, //7A to 7F
138, 139, 140, 141, 143, //8A to 8F
154, 155, 156, 157, 159, //9A to 9F
160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, //A0 to AF
176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, //B0 to BF
192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, //C0 to CF
208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, //D0 to DF
234, 235, 236, 237, 238, 239, //EA to EF
240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255: //F0 to FF
return false
}
}
} else {
return false
}
return true
}
func BenchmarkParse_5(b *testing.B) {
h := sha256.New224()
for n := 0; n < b.N; n++ {
r := rand_3(8)
h.Reset()
h.Write(r)
hash := h.Sum(nil)
if Parse_2(hash) && re.FindString(hex.EncodeToString(hash)) != ""{
//Unexpected hashes like 0e0e34567890123456789012345678901234567890123456789012 could pass the Parse_3 function so for these rare cases we can use the slow regexp check
fmt.Println(string(r))
fmt.Println(hex.EncodeToString(hash))
fmt.Println("")
}
}
}
Benchmark:
$ go test -bench . -benchmem -benchtime=5s -v
=== RUN TestParsing
--- PASS: TestParsing (0.00s)
goos: linux
goarch: amd64
BenchmarkParse_1-8 10000000 742 ns/op 280 B/op 7 allocs/op
BenchmarkParse_2-8 10000000 663 ns/op 272 B/op 6 allocs/op
BenchmarkParse_3-8 10000000 657 ns/op 144 B/op 5 allocs/op
BenchmarkParse_4-8 10000000 637 ns/op 136 B/op 4 allocs/op
BenchmarkParse_5-8 20000000 346 ns/op 40 B/op 2 allocs/op
We do not manipulate strings anymore, so the performance gap is huge. 2 times faster, 7 times fewer memory allocated than our first PoC.
EDIT: @ondrejkupka pointed out on twitter that the PoC can be further improved by allocating the random password and hash slices only once:
func rand_4(b []byte) {
n := len(b)
for i, cache, remain := n-1, src.Int63(), letterIdxMax; i >= 0; {
if remain == 0 {
cache, remain = src.Int63(), letterIdxMax
}
if idx := int(cache & letterIdxMask); idx < len(letterBytes) {
b[i] = letterBytes[idx]
i--
}
cache >>= letterIdxBits
remain--
}
}
func BenchmarkParse_6(b *testing.B) {
h := sha256.New224()
r := make([]byte, 8)
hash := make([]byte, 0, 28)
for n := 0; n < b.N; n++ {
hash = hash[:0]
rand_4(r)
h.Reset()
h.Write(r)
hash = h.Sum(hash)
if Parse_2(hash) && re.FindString(hex.EncodeToString(hash)) != "" {
//Unexpected hashes like 0e0e34567890123456789012345678901234567890123456789012 could pass the Parse_3 function so for these rare cases we can use the slow regexp check
fmt.Println(string(r))
fmt.Println(hex.EncodeToString(hash))
fmt.Println("")
}
}
}
Benchmark:
$ go test -bench . -benchmem -benchtime=5s -v
=== RUN TestParsing
--- PASS: TestParsing (0.00s)
goos: linux
goarch: amd64
BenchmarkParse_1-8 10000000 742 ns/op 280 B/op 7 allocs/op
BenchmarkParse_2-8 10000000 663 ns/op 272 B/op 6 allocs/op
BenchmarkParse_3-8 10000000 657 ns/op 144 B/op 5 allocs/op
BenchmarkParse_4-8 10000000 637 ns/op 136 B/op 4 allocs/op
BenchmarkParse_5-8 20000000 346 ns/op 40 B/op 2 allocs/op
BenchmarkParse_6-8 30000000 296 ns/op 0 B/op 0 allocs/op
That is another 15% performance increase. We now have 0 allocation per operation. Thanks @ondrejkupka!
I am not a Go specialist, this was an occasion for me to learn Go. If you find other optimizations, please tell me!
You can download the full benchmark file here.
Results
The final Go script ran on a few cheap VPS for some weeks. Here are the results:
MD5:
$ echo -n ".V;m=*]b?-" | md5sum
00e45653718969294213009554265803
$ echo -n "egNJHP66&3E1" | md5sum
00e99757454497342716194968339146
$ echo -n "KnCM6ogsNA1W" | md5sum
00e73414578113850089230341919829
$ echo -n "&rh1ls6cl&G4" | md5sum
00e48890746054592674909531744787
SHA1:
$ echo -n "&O&GKtn&54xQ" | sha1sum
00e8144605926111857621787045161777776795
$ echo -n "Sk~HOM&QzJXl" | sha1sum
00e8943083323373991014599597566984182387
SHA224:
$ echo -n "y4tIy266ToOd" | sha224sum
0e518579138232099136851755726721425672032590357318839002
$ echo -n "qE97zTka" | sha224sum
0e388554900535759017118457601686136319720227650147403334
$ echo -n "4ve1WIcJ" | sha224sum
00e45751369882124962626173083350310795241976330980564558
$ echo -n "tvzsvOfY" | sha224sum
00e75765830079753525734713212085357035084201605923734466
We obtained our Graal: 2 super magic SHA224 hashes!
Remediation
The recommendations are easy to prevent the attacks possible with super magic hashes:
- Always use strict comparison in PHP:
===instead of== - Do not use a raw binary input for the Bcrypt algorithm
php > $pass1 = 'KnCM6ogsNA1W';
php > $pass2 = '&rh1ls6cl&G4';
php > echo hash('md5', $pass1);
00e73414578113850089230341919829
php > echo hash('md5', $pass2);
00e48890746054592674909531744787
php > var_dump(hash('md5', $pass1) == hash('md5', $pass2));
bool(true)
php > var_dump(password_verify(hash('md5',$pass1, true), password_hash(hash('md5',$pass2, true), PASSWORD_DEFAULT)));
bool(true)
php > var_dump(hash('md5', $pass1) === hash('md5', $pass2));
bool(false)
php > var_dump(password_verify(hash('md5',$pass1), password_hash(hash('md5',$pass2), PASSWORD_DEFAULT)));
bool(false)
Note that super magic hashes are not only related to password storage issues; CSRF or MAC bypasses were possible thanks to these hashes.
Conclusion
We have combined 2 known vulnerabilities in order to create a new concept: super magic hashes. Such hashes can be used to detect 3 types of issues:
- Type Juggling
- Weak password storage
- Incorrect Bcrypt usage
These vulnerabilities can lead to the bypass of authentication systems.
A bit of math has shown us that these hashes are quite rare and so we tried to optimize a Go PoC. After a few weeks of calculation on cheap VPS servers, the result is here:
php > $pass1 = '4ve1WIcJ';
php > $pass2 = 'tvzsvOfY';
php > echo hash('sha224', $pass1);
00e45751369882124962626173083350310795241976330980564558
php > echo hash('sha224', $pass2);
00e75765830079753525734713212085357035084201605923734466
php > var_dump(hash('sha224', $pass1) == hash('sha224', $pass2));
bool(true)
php > var_dump(password_verify(hash('sha224',$pass1, true), password_hash(hash('sha224',$pass2, true), PASSWORD_DEFAULT)));
bool(true)
A pull request has been made to the spaze's project.
Hopefully, the quest of magic hashes will also focus on super magic hashes.
Going further
Carl Löndahl has done what was expected for many years: tweak hashcat to find magic hashes. This is a game changer as it is probably the fastest way to compute hashes nowadays. @Chick3nman512 and @hops_ch are also working on a hashcat fork to find magic hashes. Stay tuned!
Another idea is to tweak a GPU bitcoin miner, since they are designed to find specific SHA256 hashes.
For now, let's try to find SHA256 (and other algorithms) super magic hashes!
References
Magic hashes/Type Juggling:
- https://twitter.com/TihanyiNorbert/status/1138075224010833921
- https://twitter.com/spazef0rze/status/439352552443084800
- https://github.com/spaze/hashes
- https://www.whitehatsec.com/blog/magic-hashes/
- https://www.owasp.org/images/6/6b/PHPMagicTricks-TypeJuggling.pdf
Bcrypt issues:
- https://paragonie.com/blog/2016/02/how-safely-store-password-in-2016#why-bcrypt
- https://paragonie.com/blog/2015/04/secure-authentication-php-with-long-term-persistence
- https://blog.ircmaxell.com/2015/03/security-issue-combining-bcrypt-with.html
Golang optimization:
- https://stackimpact.com/blog/practical-golang-benchmarks/#numeric-conversions
- https://syslog.ravelin.com/byte-vs-string-in-go-d645b67ca7ff
- https://stackoverflow.com/questions/22892120/how-to-generate-a-random-string-of-a-fixed-length-in-go
Some ressources for people who would like to tweak hashcat to find magic hashes:
- https://grocid.net/2019/08/03/finding-magic-hashes-with-hashcat/
- https://twitter.com/Chick3nman512/status/1157748868823621638
- https://www.synopsys.com/blogs/software-security/cracking-xenforo-corpuses/
- https://hashcat.net/forum/thread-7794.html
